Remember those giants in Amar Chitra Katha or whatever your favourite superhero comic or movie featured back in the day?
They were imagined as humans, but only scaled proportionately in all directions. 10 times as high, 10 times as wide, and 10 times as thick.


But are such creatures physically possible?
Their weight would be 1000x that of a normal human, while the cross-sections of their bones would only be 100 times as big. So, each square inch of bone would now have to support 10x the weight, and the giant would break his bones by just trying to support their weight.
All of this has to do with a simple law in mathematics called the Square Cube Law.
The law describes how surface area of an object scales in proportion to its volume as its size increases or decreases.Put simply, the law states that as a shape grows in size, its volume grows faster than its surface area.
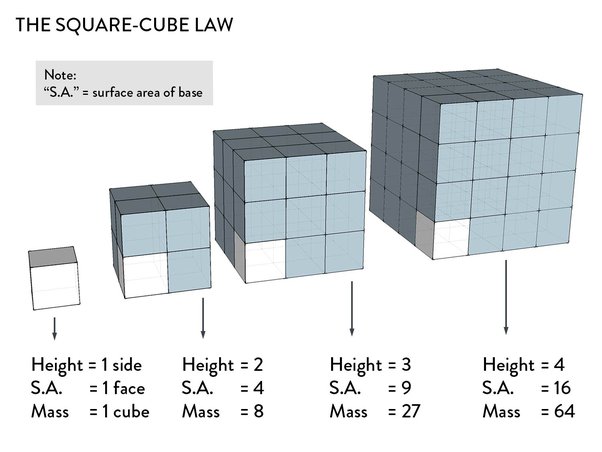
When a physical object maintains the same density and is scaled up, its volume and mass are increased by the cube of the multiplier while its surface area increases only by the square of the same multiplier.
For a fixed density, this would mean that the weight of the object grows much faster than the area along which that weight is distributed. Hence, more pressure is exerted per square inch on the surface and the magnified object would have less ability to resist stress and would be more prone to collapse under acceleration of any kind.
This is why large animals like elephants have a proportionately larger bone structure than that of a mouse, because they carry proportionately higher weight as the size scales up.
And if those giants you saw in those comics had the same bone density and structure as that of an average human, they would break their thighs every time they took a step and collapse under their own weight.
But why are we talking about giants and breaking bones?
Because it has to do with a fundamental concept in operational economics called geometric scaling.
A process often gets more efficient if the equipment for it is made physically bigger. This is due to area/volume relationships: doubling the radius of a sphere increases the surface area by a factor of 4, but increases the volume by a factor of 8.
The power developed by an engine, without speed increase, is proportional to its volume but the heat lost through its walls is proportional to the squared as it depends on the surface area of the engine, which scales squarely.
So, if you halve the engine size, you have 1/8th of the power [(1/2)^3] but a quarter of the heat loss [(1/2)^2]. Therefore a small engine will be less efficient, thermally, than a large engine as it dissipates less heat into the environment and retains more heat for better combustion. Engines have costs that rise in proportion to surface area but power that rises in proportion to volume, making larger engines cheaper on a per-output basis.
Even processing equipment in chemical factories and oil refineries often has costs that rise in proportion to surface area, but output that rises in proportion to volume.
Let's consider the shipping industry and how it benefits from geometric scaling.
According to research conducted by the United States Merchant Marine Academy, today the largest container ships are capable of carrying over 19000 twenty-foot equivalent units (TEU), and orders have already been placed for ships with capacities of over 21000 TEU — which means the ship can accommodate 21000 20-foot long shipping containers.
In 1995, the average container ship had a maximum capacity of 1498 TEU. By 2005, this had increased to 2171 TEU, and by 2015 it was 3649 TEU.
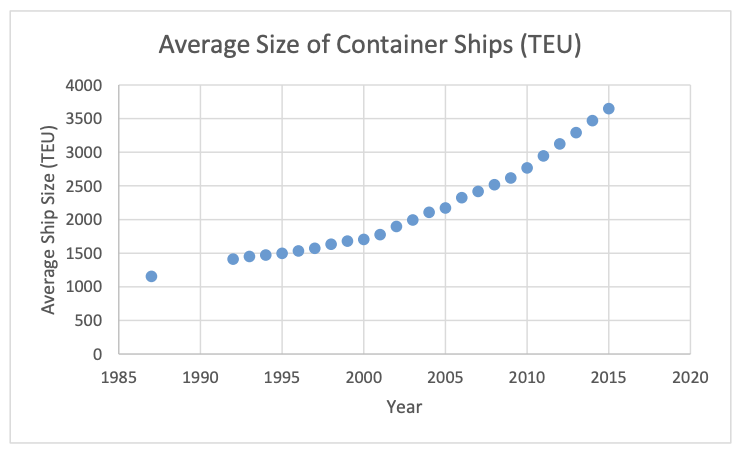
So, what led to a gradual increase in the sizes and capacities of these cargo ships?
Well, ship owners wanted to minimize the cost per TEU in order to get more business as the demand for containerized freight and global consumer-driven shipping increased over the years.
They could either do that by building more ships or increasing the size of those already built. And ship owners had good reasons to believe that mega-ships offer a cost advantage in the long term even though the one-time cost of building these ships is huge. And a lot of it has to do with economies of scale, specifically those that arise due to the benefits of geometric scaling and the square-cube law.
If you double the length of a ship and keep its proportions the same, the resistance to motion through the water will increase by the square, four times, but the carrying capacity by the cube, eight times.
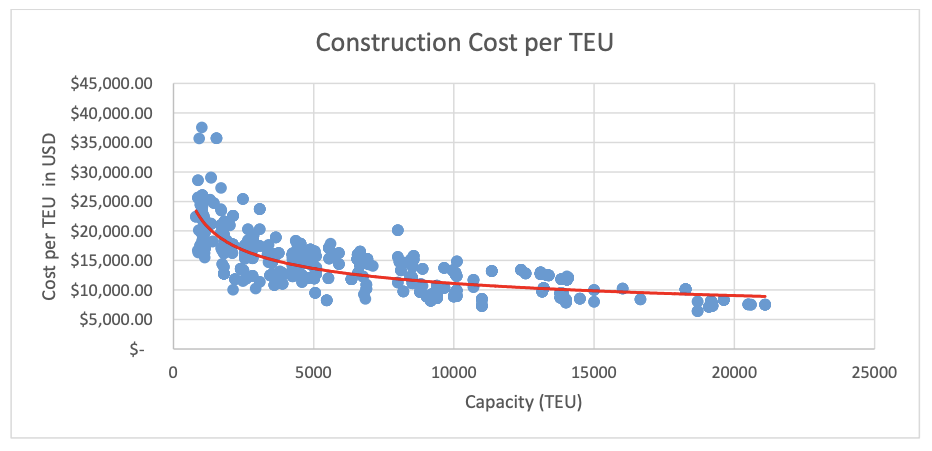
Not just that, smaller ships cost more to build per TEU; a ship of 6000 TEU costs, on average $13,912 per TEU while a ship over 13300 TEU has a per TEU cost of just $9,299.
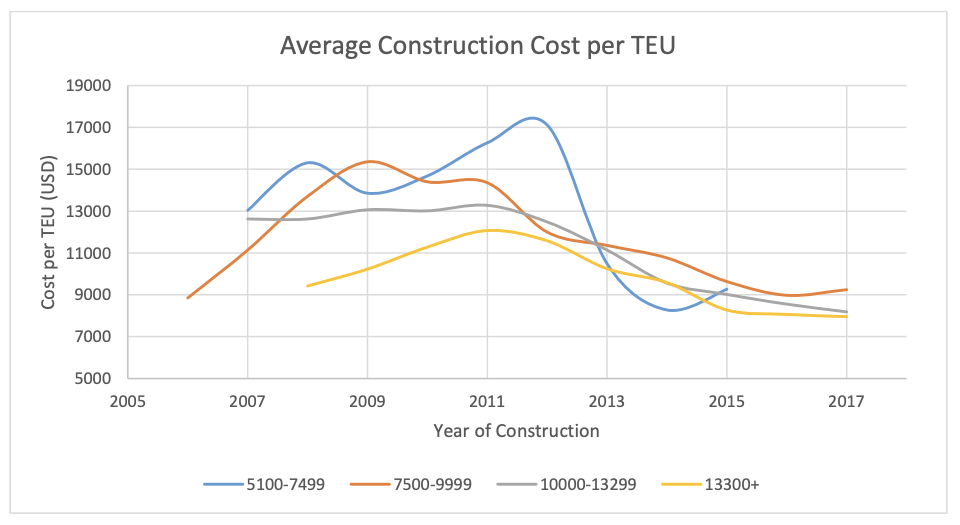
Even operating costs per TEU fall with increasing ship size. The graph below shows the operating costs per TEU for the years 2001, 2008, and 2015 (values are not inflation-adjusted).
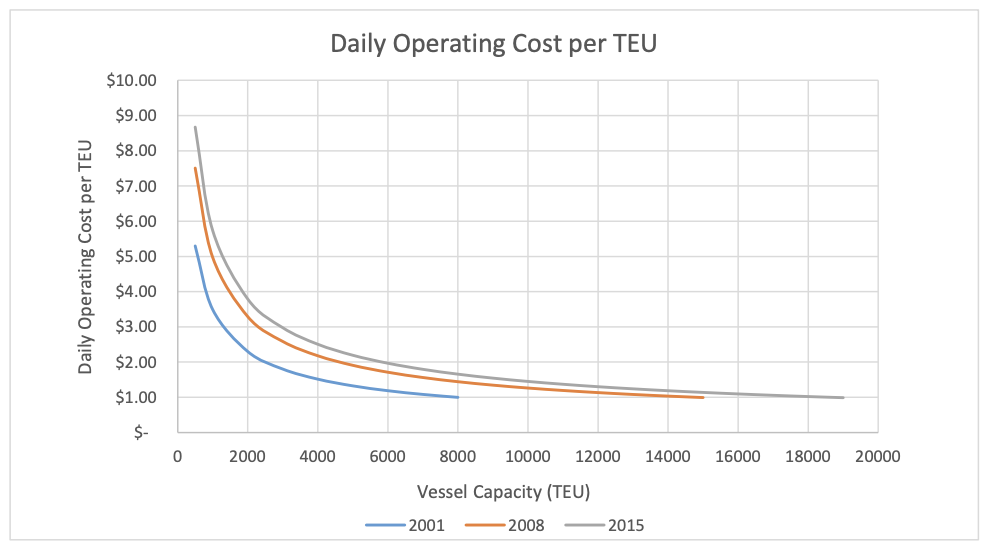
It is apparent that larger ships have considerably lower per TEU costs than smaller ones; again, the economy of scale persists. In 2015, a 5000 TEU vessel had a daily per TEU operating cost of $2.19, a 10000 TEU ship a cost of $1.45, and a 15000 TEU ship of $1.14.
Container ships show geometric scaling in both construction costs — due to costs scaling with surface area and capacity scaling with volume — and operating costs — due to larger engines and proportionally less fuel consumption. What you see is a steady increase in shipping batch size: increasingly larger ships moving increasingly large numbers of containers at once.
Are there domains where geometric scaling leads to diseconomies of scale, i.e., as the scale increases, per unit cost also increases?
Yes. Building construction is one such domain.
Each additional floor adds load to the floor below, and these lateral forces rise non-linearly with height: bending moments rise with the square of height; sway and deflection moments rise with height to the 4th power, requiring heavier structural framing and more elaborate foundations.
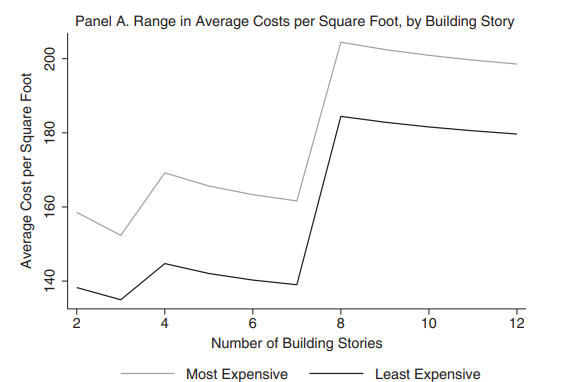
Also, the taller a building gets, the more complex and expensive its truss becomes, the more it costs to move people and materials to the top, and the longer it takes to construct every added floor. You need more elevators, better fire safety and egress facilities, and just proportionally more and better infrastructure in general.
Similarly, crane size and expense scale linearly with building size: larger buildings tend to need larger and/or more expensive cranes and sometimes just more of those cranes.
The economies of scale you benefit from when you order larger batches of material aren't enough to offset these growing costs that come with every floor that gets added. But these are one-time costs and ultimately get transferred to the customer when they buy a flat in one of these high-rises. It is supply acting in line with demand, so you still tend to see more high rises over time.
There are still many concepts to discuss in logistics and operations but I'll cut it here for now.
Do remember this concept of geometric scaling as we discuss more operational and logistical concepts in the coming days and weeks. We'll refer back to it many times in the near future.
And yes, let me tell you why yo mama so fat.
Because the larger she grows, her volume grows faster than her surface area. And heat dissipation is directly proportional to the surface area of the object, which means that the fatter she grows, the more heat she retains.
Yo mama so fat because it makes her hotter. Literally.
(No offense intended to mama ❤️)












