In the first part of Strategy Essentials, we got down to brass stacks of what makes a sound strategy.
I delved into the idea that a significant part of any strategy is decision-making. And that good decision-making reduces the number of decisions to be made in the future.
We discussed that to be good at strategising, one must identify the players, the resources each player has access to, the rewards they’re playing for, and how they arrive at an equilibrium state.
In the example of traffic jams, I highlighted that the optimal strategy would help both you and Raj navigate without any accidents and without delaying the commute for the other.
In the case where two businesses compete, the optimal strategy is to price similar products in a way that disincentivizes players from defecting because the rewards don’t improve significantly even if the player defects.
Both these examples end in a state where players reach the best choice that mutually benefits both players. It is what one would call a win-win case. A game theorist would label this state as Nash equilibrium.
Typically, Nash equilibrium describes a situation where no player can improve their outcome by changing their strategy, given the strategies of the other players.
But do all gameplays arrive at Nash equilibrium?
Not necessarily.
Consider a tic-tac-toe game. In a standard game, player one (X) and player two (O) are each trying to make 3 in a row. If both play optimally, the game ends in a draw.
Now consider a variation: Player one wins if either Xs or Os make 3 in a row, and Player two wins only if the board ends in a draw. Now who wins the game?
Let’s suppose I am player one and mark X in the centre square.

You can either play in a corner or an edge. Either way, I can force a win in just a few moves. Let’s go through the cases.
(a) You play a corner

Now I can play in either adjacent corner to where you played (not the opposite corner). In this case, I play in the bottom-left corner.

You block by putting an O in the first row.

Now I can play in the third-row middle column, creating a double attack.

You are stuck. Either you block the three in a row of Xs, thereby making three Os in a row. Or you move elsewhere, allowing me to make three Xs in a row on the next turn. Let’s consider another case.
(b) You play an edge

Now I play in an adjacent corner to your move. In this case, the upper right corner is taken.
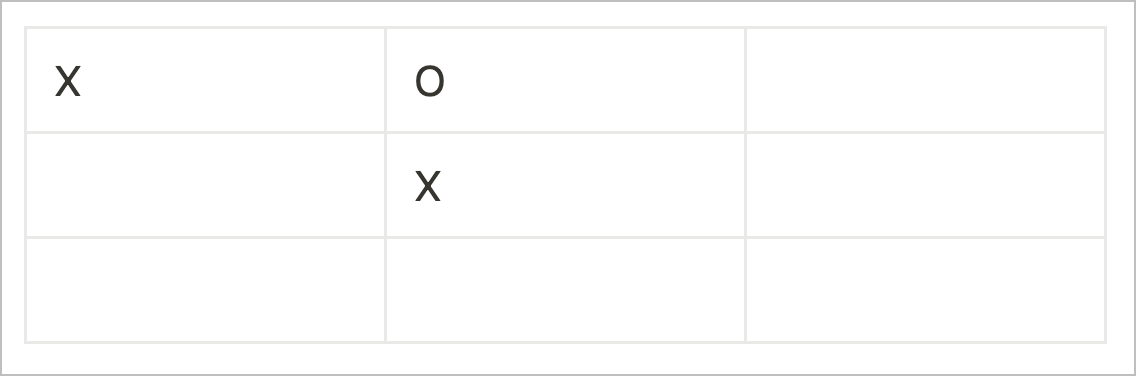
You have to block.
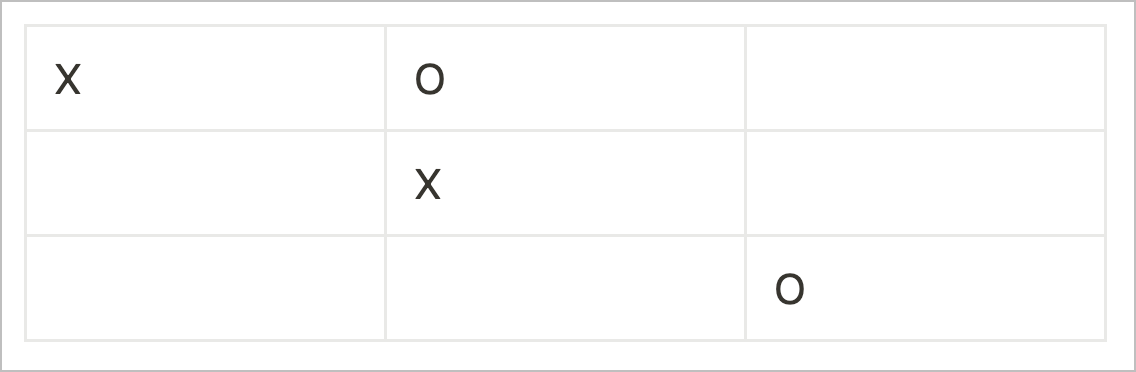
And this allows me to create a double attack by playing in the edge adjacent to Xs in the corner and the centre.
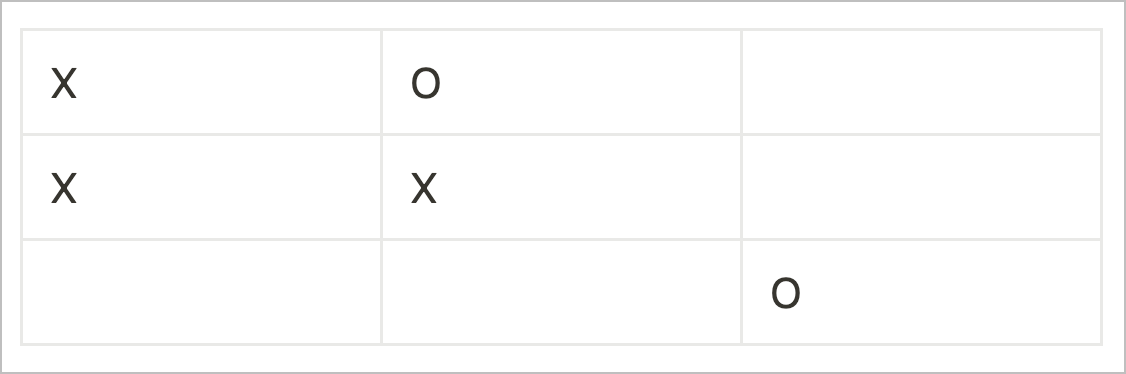
Just like in regular tic-tac-toe, player two cannot block both attacks and loses.
Player Two is resigned to reacting to the choice made by Player One till Player One wins.
Unlike in the case of Nash equilibrium, where both players had to arrive at a strategy that benefitted both simultaneously, in some game plays, one player can have a dominant strategy and the other can’t.
Now who enjoys a chance at playing a dominant strategy is usually decided by the payoff or reward structure that rules the game.
For instance, in the tic-tac-toe game, one player was incentivized to get either three Xs or three Os in a row, whereas the other player’s incentive was to find a way to draw the match. The incentives set off the players to make choices where player one had an edge over the other simply by picking the first move.
Sure, you might argue that this example is too constrained, so let’s look at a few more cases where such gameplay involving dominant strategies occurs.
There are two firms in a market that are deciding whether to run an advertising campaign or not. The maximum profit any firm can earn is 28 units. Based on the choices both firms have to make and how much profit can be earned, we draw up a payoff matrix reflecting the outcomes for each firm.
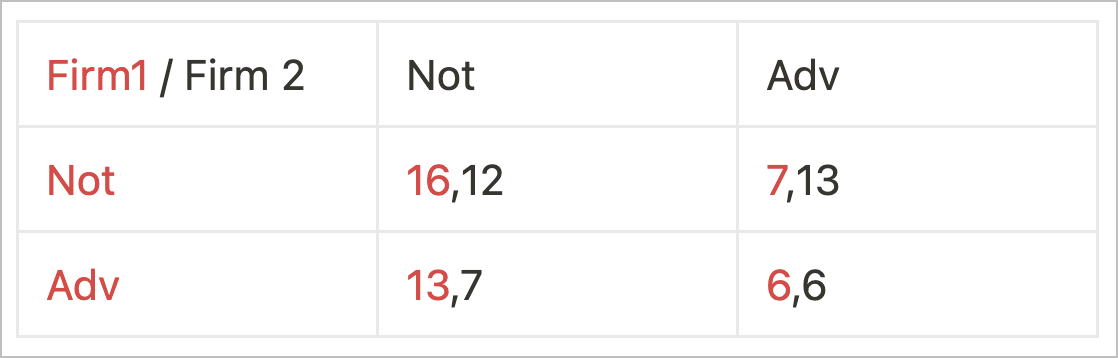
But for the payoff matrix to make sense, you will have to account for the following assumptions about the market —
- From the not-not option, we learn that firm 1 is bigger than firm 2 by 16:12. It basically reflects a market state where both firms don’t advertise, and yet firm one earns more profits.
- The cost of advertising is 8 units
- If only one advertises, it gets a 75% market share
- If both advertise, both get 50% – 50%
So, if you were to look at the choice where either one of the firms advertises, the payoff is (13,7) or (7,13) because
75% of 28 = 21
21 – 8 (Advertising cost) = 13
Now in order to analyse who has a dominating strategy in this game, let’s look at each firm’s choices individually.
Choice 1 — When firm one doesn’t advertise, it earns a profit of 16 units and 7 units. In the case where firm two also doesn’t advertise, firm one wins the game (16,12). In the case where firm two advertises, it loses market share but saves on advertising spending.
Choice 2 — When firm one advertises, it earns a profit of 13 units or 6 units. If only firm one advertises, it regains market share and earns 13 units but loses advertising money and earns 6 units when both firms advertise.
If you look carefully, you will notice that firm one’s choice to not advertise, illustrated in Choice 1, reflects a dominant strategy. When firm one decides not to advertise, it earns more profits and therefore keeps making that choice regardless of the choice of firm two. (16 > 13) (7 > 6)
For firm two, the rewards are opposite in direction. Look at 12 units and 13 units or 7 units and 6 units in the bottom row. Once firm two realises that without advertising, it stands to lose in the market, it reacts by advertising and increasing its revenue to 13 units.
Firm two reacts to firm one’s move. But once firm two reacts, firm one is also locked into the not advertising strategy because if firm one reacts to firm two by advertising, both lose and arrive at lowered rewards of 6 units each.
Firm one continues to play the not advertising game even though it is sub-optimal for both players because the rewards for firm one are best aligned with that choice. Firm two ends up as a second fiddle because it is constantly reacting to the moves made by firm one in order to increase its rewards.
This happens because the rewards for both players in the game are highly individualistic.
For firm one, the reward is to sustain its dominant position, provoking firm two to react and spend money. Firm one doesn’t lose much when it decides not to advertise. Because even if firm one has a lower market share, the money it saves by not advertising can be spent on further product research; it can be used to hire better talent or technology. By not spending on advertising, it is in a position to invest in the future, thereby cementing its dominant position.
However, this example is of the kind where only one player has an edge of some kind over the other and can therefore play dominant. But there is a popular case where both players can enjoy a chance at a dominant strategy — The Prisoner’s Dilemma.
In the case of Prisoner’s Dilemma, two criminals are arrested and interrogated in separate rooms.
The authorities have no other witnesses and can only prove the case against them if they can convince at least one of the criminals to betray their accomplices and testify to the crime.
Each criminal is faced with the choice to cooperate with their accomplice and remain silent or to defect from the gang and testify for the prosecution.
If they both co-operate and remain silent, then the authorities will only be able to convict them on a lesser charge resulting in one year in jail for each (1 year Criminal 1 + 1 year for Criminal 2 = 2 years total jail time).
If one confesses and the other does not, then the one who testifies will go free, and the other will get five years (0 years for the one who defects + 5 for the one convicted = 5 years total).
However, if both testify against the other, each will get three years in jail for being partly responsible for the crime (3 years for Criminal 1 + 3 years for Criminal 2 = 6 years total jail time).
The respective penalties can be expressed visually as follows:

In this case, each criminal always has an incentive to defect, regardless of the choice the other makes.
From criminal 1’s point of view, if criminal 2 remains silent, then criminal 1 can either cooperate with criminal 2 and do a year in jail or defect and go free. Obviously, she would be better off betraying criminal 2 in this case. On the other hand, if criminal 2 defects and testifies against criminal 1, then criminal 1’s choice is either to remain silent and do five years or to talk and do three years in jail.
Again, obviously, criminal 1 would prefer to do the three years over five.
In both cases, whether criminal 1 cooperates with criminal 2 or defects to the prosecution, criminal 1 will be better off if they defect and testify.
Now, since Criminal 2 faces the exact same set of choices, he will always be better off defecting as well.
The paradox of the prisoner’s dilemma is this: both criminals can minimize the total jail time that the two of them will do only if they both cooperate and stay silent (two years total), but the incentives that they each face separately will always drive them each to defect and end up doing the maximum total jail time between the two of them of six years total.
In the prisoner’s dilemma, the incentives are the same for both players, but an inability to gauge what the other player will pick and defect leads to an outcome which is sub-optimal for both players. So, even though both players can play dominant by cooperating and choosing an optimal outcome, their individual incentives pull them in the opposite direction leading to a sub-optimal outcome.
But then, how is a dominant strategy different from a Nash equilibrium?
Well, a dominant strategy is a strategy that is better than any other strategy for one player, regardless of what strategies the other players choose. It means that the player with a dominant strategy can always get the best possible outcome, no matter what the other players do.
Whereas, a Nash equilibrium is a situation where no player can improve their payoff by changing their strategy, given the strategies of the other players. It means that the players are in a state of mutual best response, where each player’s strategy is optimal given the other players’ strategies.
In a dominant strategy, one player has the power to sway the game for his benefit, as in the case of Nash equilibrium, one player cannot enjoy benefits without the cooperation of another player.
Put differently, a dominant strategy is like a winning move in a game, where you can always win regardless of what your opponent does. Nash equilibrium, on the other hand, is like a stalemate in a game, where neither you nor your opponent can win by changing your existing strategy.
Given all this download, I am sure you’re wondering if one can predict which strategy will work out for any given situation. I will discuss this in the following piece.
Stay tuned!












