So many of you mention strategy as an interest when subscribing to Stoa Daily. I get countless LinkedIn messages from people asking for a “strategy” role at Stoa.
So far, I’ve masked my disdain for those who use strategy or strategy roles as a proxy for not doing other kinds of scrappy work; for not getting their hands dirty in the messiness of execution.
So, today, let me just attempt to unwrap one important part of strategy:
Game Theory.
Or Game Theoretic Thinking, to be more precise.
Now I know, the term sounds quite fancy — and it is fancy if you were to go down to the math of it (it's a whole complex field of mathematics in itself) — but anyone can practice basic game-theoretic thinking, even without going into the math.
If you were to pull off the fancy veneer from strategy, you would realize that it is nothing but plain critical thinking, that accounts for all the important variables in any given problem. We are all strategizing in one way or another all the time, outside of work too. It's just a difference in stakes and the complexity you're dealing with.
When you plan a trip with your friends, you are doing some form of strategy, except the stakes are lower, the complexity is lower. If you do it well, only you and your friends have a good trip, and your friends trust you to plan more trips in the future.
Being a “strategy leader” in the business context earns you more acclaim. Simply because the stakes are higher and you're dealing with a lot more uncertainty.
However, the skillset you're exhibiting in any strategy role, fundamentally, is just good decision-making. And making good decisions consistently is tough.
Today, let's explore one aspect of strategic thinking: Game Theory.
Suppose you are driving, and Raj is driving the car behind you. You both are approaching an intersection with a traffic light that is about to turn red.
You both have to decide whether to stop or go through the intersection.
- If you both stop and cooperate, you avoid a collision and incur a small delay.
- If you both go through the intersection, you get into an accident and incur a large delay.
- If you decide to stop and Raj goes through the intersection, you incur a large delay, and Raj avoids a delay.
- If you decide to go through, but Raj stops, you reach your destination faster and Raj has to wait.
From a strategy standpoint, what’s happening is —
You and Raj are players in a traffic jam. You both have certain resources at your disposal —the type of car, your driving skill, how much you care about traffic rules and so on. Both of you must reach a destination(reward), but Raj has much to lose because he is late for a meeting.
Based on these conditions, both of you will make a certain set of decisions.
Each decision a person makes will impact not only the person who made the decision but also the other players and vehicles in the traffic jam.
The stakes might not be as high or have a monetary value as in the case of business decisions, but in the given context, they are crucial.
The outcome of each decision will mean different rewards for the players in this traffic jam. For instance, if Raj decides to overtake you, the decision ensures he avoids a delay, but it is at the cost of keeping you stuck in the traffic jam for a few more minutes.
You essentially pay for his delay by the time you spend waiting.
I am sure you’ve noticed this form of interaction in your daily commute. Additionally, unlike in this example, where only two players interact, in a real-life traffic jam, multiple players with different vehicles interact at the same time. No wonder the chaos!
An ideal case would be if you and Raj both navigate without any accidents and without delaying the commute for the other. It is certainly idealistic to expect that, but that is what a strategist would call an optimal equilibrium state.
If the decisions made by you and Raj reach an equilibrium state, you basically arrive at a point where you don’t have to change your strategy, because it doesn’t improve your reward function without having the other player change their strategy — which would make you both worse off than from where you started.
If all players are better off and no one can increase their reward function without others retaliating, then you are at an optimal equilibrium. If all players are worse off, and no one can increase their reward function without taking up significant cost or risk, then you're at a sub-optimal equilibrium.
For example, suppose there are two competing companies, Company A and Company B, in the same industry. Both companies sell a similar product to a shared customer base.
Initially, Company A decides to lower its prices in order to gain a competitive advantage. As a result, the customers flock to Company A and its sales skyrocket. In this situation, Company A benefits from increased profits and customer loyalty, as its reward function is maximized.
Company B, realizing that its customer base is dwindling, decides to respond by lowering its prices as well. This leads to intensified competition and a price war between the two companies. Both companies are worse off in this scenario, as they are experiencing reduced profits due to lower prices and increased costs associated with marketing and promotional activities.
This represents a sub-optimal equilibrium, as both companies are worse off than before the price war.
However, if both companies reach a point where reducing prices further would no longer yield any significant benefits, they may decide to maintain their current pricing strategies. By avoiding further price cuts, they can prevent a further decline in their profit margins.
This can be considered an optimal equilibrium, as neither company can increase its reward function without the other retaliating. In this case, both companies are better off than in the sub-optimal equilibrium of the price war, although they may not be maximizing their profits individually.
Now, game theory operates in all contexts around you, and I feel you would benefit from grasping even the non-business contexts of game theory, which will help you think of it from a more practical perspective.
For this, David Easley and Jon Kleinberg’s Networks, Crowds, and Markets offers a brilliant example.
“Evolutionary biology is based on the idea that an organism’s genes largely determine its observable characteristics, and hence its fitness, in a given environment.
Organisms that are more fit will tend to produce more offspring, causing genes that provide greater fitness to increase their representation in the population.
In this way, fitter genes tend to win over time, because they provide higher rates of reproduction.
The key insight of evolutionary game theory is that many behaviors involve the interaction of multiple organisms in a population, and the success of any one of these organisms depends on how its behavior interacts with that of others.
So the fitness of an individual organism can’t be measured in isolation; rather it has to be evaluated in the context of the full population in which it lives.
This approach opens the door to a natural game-theoretic analogy: an organism’s genetically determined characteristics and behaviors are like its strategy in a game, its fitness is like its payoff, and this payoff depends on the strategies (characteristics) of the organisms with which it interacts.”
Basically, even how our genetic behaviours evolve is similar to the way our genes (players) interact with other players using resources to make decisions that increase the chances of the organism’s survival. The increase in the likelihood of survival and reproduction is the reward for the genes.
In fact, how genes strategize and reach a state of equilibrium — reduced to minimal decision-making — is a useful way to predict the evolution results in a population.
For instance, let’s consider a particular beetle species and suppose its fitness in a given environment is determined by how much food it can find and how many nutrients it extracts.
Now, a particular mutation is introduced into the population, causing beetles with the mutation to grow to a significantly larger body size. Thus, we now have two distinct kinds of beetles in the population — small ones and large ones.
The large beetles, by design, have a high metabolic requirement and, therefore, must divert more nutrients from the food they eat, negatively impacting their fitness.
A logical conclusion that would follow is that the large-body-size mutation is fitness decreasing, and so it will likely be driven out of the population over time through multiple generations.
But here’s what actually takes place —
Beetles of different sizes compete with each other for food. Unsurprisingly, beetles with large body sizes are more effective at claiming an above-average share of the food.
Assuming a pair of beetles, similar in size, compete for food, it gives rise to the possibilities in the matrix:

We are assigning a numerical reward to the fitness that each beetle gets from a food-related interaction in this game.
- When beetles of the same size compete, they get equal food shares. Look at the (5,5) (3,3) combinations in the matrix
- When a large beetle competes with a small beetle, the large beetle gets the majority of the food. Look at the (1,8) (8,1) combinations in the matrix
- In all cases, large beetles experience less of a fitness benefit from a given quantity of food since some of it is diverted into maintaining their expensive metabolism.
In a two-player game between the first beetle and the second beetle, their body size is the resource each player (beetle) uses to extract nutrients (reward).
Consequently, the equilibrium state in this game would be the subsequent evolution of an ideal beetle size that can extract nutrients in the most efficient way possible.
The only major difference between this example and the traffic jam one is that the beetles in this game aren’t asking themselves,
“What do I want my body size to be in this interaction?”
Rather, each is genetically hardwired by evolution to survive and reproduce, and by virtue of it, iterate through multiple mutations to maximize fitness. And their eventual survival or extinction will depend on not just these two beetle types, but how they're able to co-exist and mutate in a complex ecosystem with hundreds of other variables at play — some conducive to their fitness and some not.
But in both the game examples discussed above, certain aspects are consistent:
- players
- strategies
- rewards or payoffs
- equilibrium states
These are the fundamental concepts you must wrestle with when exercising game-theoretic thinking.
Have you wondered...
Why are all hotels clustered up together in a single location in any city?
Why are all pubs and bars often in the same lane?
Why are all electronics and hardware shops established in a single location like Lamington Road in Mumbai or Connaught Circle in Delhi?
You might question why, for the sake of consumer convenience, these businesses aren't spread all across the city at regular distances from each other.
Well, this phenomenon is just an example of iterative game theory leading to a sub-optimal equilibrium. In their quest to gain a higher share of the market, businesses of the same kind eventually all end up opening in the same locality.
Of course, there are other economies at play here that make such an arrangement advantageous. But a lot of it has to do with simple iterative game theory leading to such an equilibrium.
Competing businesses should, in theory, locate far apart from each other to serve their customers while minimizing customer commute time. But in reality, they colocate because customers will travel for:
- Better selection
- Better prices driven by competition
- Economies of scale that develop around clusters of competing businesses which allows them to become more competitive
This is basically why all the furniture shops end up located in one part of town or why we have farmers' markets.
Each shop tries to maximise the customers it caters to without ruffling the competition too much. Invariably, they arrive at a state where shops are located very close to each other and often offer similar products at identical prices.
To understand how this happens, watch this YouTube video that uses the example of two competing ice cream vendors at a beach to explain why even after employing multiple strategies to maximize market share, both players eventually arrive at an equilibrium where they're both huddled up in one single area of the beach.
Here's another example:
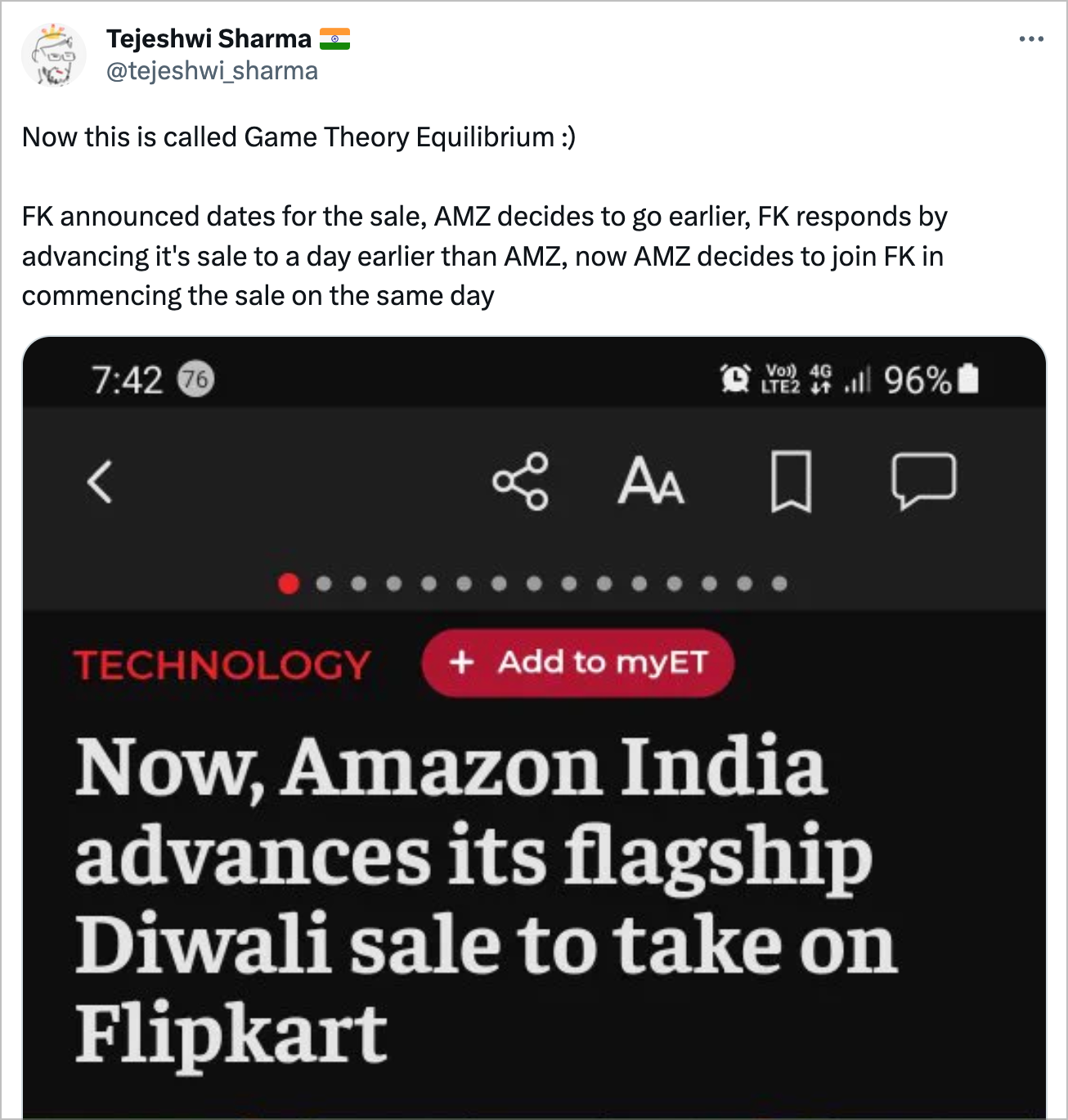
When businesses reach this stage after constantly playing the action-reaction game, the industry has usually matured, customers are aware, and the decision cycles slow down. Brands constantly making new decisions become inefficient, and so the next set of changes arrives only when an externally enforced significant variable pushes players out of this equilibrium state.
But the gist of game-theoretic thinking is:
To make good decisions, every player in a given market must be cognizant of how the other players will react to any given move. If you are someone who struggles with simple decision-making, a way to improve that would be to take on the frame of game theory and objectively list down:
- other players within your context
- the access to resources each player has and what they risk losing
- the rewards that align players in the market, e.g. market share, top-of-mind share, share-of-wallet, etc.
- potential equilibrium states for the game or market in question
If you practise this exercise long enough, I assure you that you’ll be able to see every context you inhabit as some form of game theory at play. I can go so far as to say that it is the frame you won’t be able to unsee.
You will realise strategy isn’t just a role but a way of life and that you can practise in all contexts and situations. You will also become more aware of different scenarios in everyday life where some form of game theory is at play.
Finally, you will build more veneration for strategic leadership roles and realize that you need to spend YEARS in an industry to be even slightly good at making high-stakes decisions.
Strategy is not something you’ll be hired to do right off the bat.
If you want a good overview of what your career will look like and at what stage strategy will come into the picture, read this essay.
You might also like reading these:












